IMU Accelerometer Measurements with Respect to a Static Coordinate System
Overview
Inertial measurement units (IMUs) are useful measurement devices that contain magnetometers, gyroscopes, and accelerometers. These tools can accurately quantify accelerational forces, however, they always report these forces with respect to their own coordinate systems. This means that as soon as the orientation of these chips change, so do their reported accelerational forces. This is a limitation of these chips because in many cases, humans find it more intuitive to express the acceleration of objects with respect to the Earth. Thankfully, this correction to an Earth frame is possible with a few mathematical tricks. Deriving the chips orientation from its sensors and rotating the acceleration vector by the corrected frame allows accurate real-time algorithms to output intuitive accelerometer data in three-dimensional space.
Madgwick Filtering
The combination of the three sensor measurements on most IMU chips (accelerometers, gyroscopes and magnetometers) allow for the precise calculation of orientation that are not explicitly reported by the IMU itself. One such technique is known as Madgwick filtering, and returns the chip’s orientation as a quaternion, a sum of complex and imaginary parts. These quaternions are mathematically represented by a+bi+cj+dk, where a, b. c, and d are real numbers and i, j, and k are complex numbers that can be interpreted as vectors along the three dimensional axes. Quaternions are preferable to Euler angles when representing orientation because they are immune to gimbal lock.
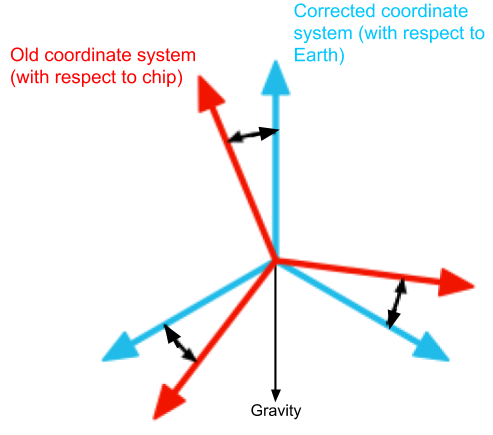
Earth Frame Correction
Applying Madgwick filtering to the IMU gives an accurate representation of the chip’s orientation in real-time. As the chip rotates, the quaternion will express this, giving us the correction to apply to the acceleration measurements. Linear algebra can be employed to apply this correction to the 3D acceleration vector, rotating the measurements to a world frame. I’m currently working on updating this page with a mathematical explanation but the simple theory is only explained here, for now. To see this algorithm applied, visit my GitHub wave height measurement repository.