Comparing Process Control Algorithms in C++

Introduction

Autonomous process controllers are used in critical infrastructure to establish desired system states, preventing equipment failure and allowing for successful process completion. A large number of these controllers use one or more parts of a comprehensive algorithm to compute a response to the system state. This equation is known as the proportional, integral and derivative control algorithm, named for each of its three fundamental parts.

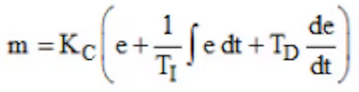
The application of this equation varies for every use case and I’ve written some C++ code to illustrate how each term changes the system performance.

Proportional Control

Proportional control uses only the first two variables of the equation, eliminating the derivative and integral terms. In this case, the equation becomes m = Kc(e). This is ideal for simple systems that do not experience persistent disturbances from the desired system state. For example, if we run the C++ simulation with this equation and no system disturbances, the process quickly reaches the desired value.

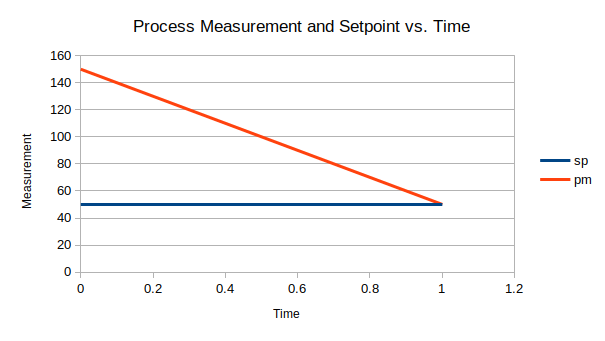
The algorithm generates an efficient controller response, causing the process to reach the desired setpoint of 50.0 within only one full time step. However, if the system is perturbed consistently off of the setpoint, the proportional algorithm is unable to reach the desired value until this error is eliminated.

For example, I introduced a function to persistently disturb the system by one measurement unit for the first eight time steps. The proportional control algorithm was only able to achieve the desired system state after this error had ceased. The entire time the error was present, the system hovered slightly above the setpoint, unable to correct for this problem.

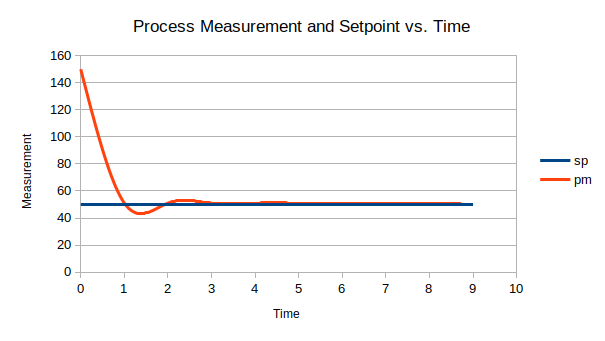
This inability to perform error correction is where the rest of the equation terms start to come in handy.

Proportional and Integral Control

By introducing the integral term into the equation we gain the ability to account for error in the system. Look what happens when we introduce this term into the simulation in a similar situation.

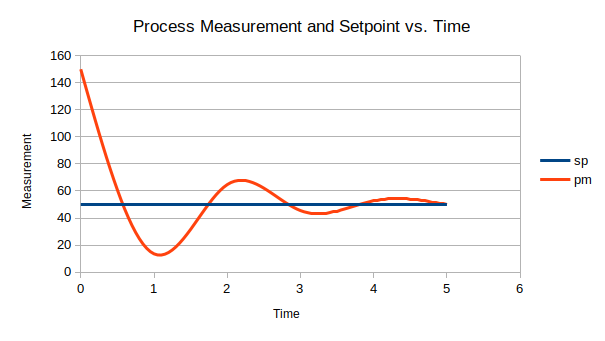
This time the controller responded to the system disturbance, allowing the process to reach the desired value even with the error being actively added into the system. This is a massive improvement to the controller response and is why proportional controllers by themselves are a rare occurrence.

Proportional, Integral and Derivative Control

Adding the final derivative term to the control algorithm results in a similar process measurement curve and increases the magnitude of the controller response. However, noisy process measurement signals can cause this term to have undesired effects, potentially driving the system away from the setpoint. Therefore, the derivative term must be carefully introduced and tuned if used in the controller.

Conclusion

The PID algorithm is an indispensible tool in process controls and allows for significant controller customizability for various use cases. Modifying the gain, time coefficients, and structure of the equation allows for an infinite number of possible controller responses. Proportional control is great for simple systems where running off setpoint is not a problem. For more precise applications, the integral and derivative terms may be introduced to further correct for system error. Currently, researchers are exploring further optimizations for this algorithm in modern computer systems.